
“用于存储和处理大量数据的服务器场(server farm)的出现引发了人们对高效、紧凑的硬件基础设施的兴趣。 电源设计人员需要进行仿真以评估权衡选择电感、开关频率、电流检测增益等参数,同时优化系统性能指标如功率因数(PF)、总谐波失真(THD)、控制回路带宽和相位裕度。
”作者:安森美半导体应用工程师Nikhilesh Kamath
用于存储和处理大量数据的服务器场(server farm)的出现引发了人们对高效、紧凑的硬件基础设施的兴趣。 电源设计人员需要进行仿真以评估权衡选择电感、开关频率、电流检测增益等参数,同时优化系统性能指标如功率因数(PF)、总谐波失真(THD)、控制回路带宽和相位裕度。 通常在数控电源中,很容易无视系统中各个点的增益,例如,在将浮点补偿器系数转换为定点形式时。本文旨在为采用数字平均电流模式控制方案进行设计的工程师提供指南,这种控制方案常用于大功率PFC应用中。
仿真通常要在运行时间和准确性之间进行权衡。 较小的仿真步长将产生更准确的结果,但需要更长时间才能完成仿真。 本文探讨使用MATLAB®建模500 W平均电流模式控制的功率因数校正(PFC)电路的步骤,MATLAB具有类似于SPICE的电路求解器。 我们使用SimscapeTMElectricalTM工具包中的功率级元器件来仿真开关模型。 Simscape工具包是Simulink®编程环境的扩展功能,并提供建模一个物理系统 (我们这里是电气系统) 的便捷方法。 我们在Simulink环境中开发了一个平均模型来分析系统稳定性。 MATLAB软件的数据处理能力允许通过脚本运行和数据记录来对仿真模型进行参数化;这在我们生活的基于数据作决策的世界中至关重要。
表1:服务器电源规格示例 [1]
|
输入交流(AC)电压范围 |
180 至 265 VAC |
|
输入AC 频率 |
60 Hz (典型值) |
|
功率因数(PF) |
> 0.97,满载的30% 至100% |
|
总谐波失真(THD) |
< 5%,满载的50%至100% |
|
能效 |
峰值能效> 97%,满载的30% 至100% |
表2:仿真系统参数
|
输入AC 电压 |
230 VAC |
|
输入AC 频率 |
60 Hz |
|
输出电压 |
384 V |
|
输出功率 |
500 W |
|
升压电感 |
500 µH |
|
脉宽调制(PWM) 开关频率 |
100 kHz |
|
输出电容 |
220 µF |
|
电流检测比 |
0.62 |
图1是个数控PFC的高级框图。 外部电压回路调节输出电压 (体电压),而内部电流回路则将检测到的电感器电流与电流基准进行比较来帮助形成输入电流,电流基准是由电压回路输出与整流线路电压相乘得出。快速模拟比较器用于逐周期过流保护 (OCP)。 下面分析了各种负载下的电压和电流回路,因为PFC是前端转换器,后面根据应用可接恒定功率、恒定电流或恒定电阻级。
电压回路分析
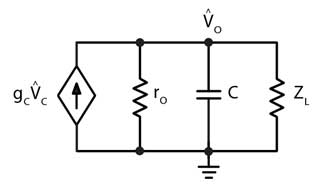
图2:升压功率因数校正电路的简化小信号电路模型
Ray Ridley博士于1987年开发了升压功率因数电路[2]的小信号电路模型。电感器电流跟踪的电流参考源于线路电压。 忽略由于输入电压引起的干扰,该电路简化为图2所示的网络,并且对输出传递函数的控制由下式给出:![]() -> 方程式[1]
-> 方程式[1]
其中:
ZL是负载阻抗
rO是小信号输出电阻,由![]() 得出
得出
C是输出电容
gC是个常数,由![]() 得出,其中
得出,其中![]() 是线性电压比例因子[2]
是线性电压比例因子[2]
对于恒定电阻的负载,ZL = RL, (rO // ZL) = RL/2:![]() -> 方程式[2]
-> 方程式[2]
对于恒定电流的负载,ZL = ∞, (rO // ZL) = rO:![]() -> 方程式 [3]
-> 方程式 [3]
对于恒定功率的辅助,ZL = -VO / IO = -rO, (rO // ZL) = ∞:![]() -> 方程式[4]
-> 方程式[4]
将以下关系式[2]代入方程式[2], [3]和[4]:![]()
![]() , 其中 M 是转换比,由
, 其中 M 是转换比,由![]() 得出
得出
我们得出了![]() 的传递函数:
的传递函数:![]() 对于恒定电阻的负载
对于恒定电阻的负载![]() 对于恒定电流的负载
对于恒定电流的负载![]() 对于恒定功率的负载
对于恒定功率的负载
表3显示受控对象的传递函数,我们系统参数是:C = 220 µF, VIN = 230 VAC, VO = 384 V, RL = 295 Ω, IO = 1.3 A.
表3:不同负载模型的受控对象传递函数
|
负载模型: |
极点位置: |
波特图: |
|
恒定电阻: |
|
|
|
恒定电流: |
|
|
|
恒定功率: |
|
|
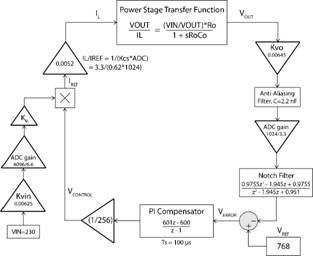
图3:恒定电流的受控模型电压回路框图
图3是前面所示的简化的升压转换器的电压回路框图。
KVIN代表外部电阻分压器增益(比率为160:1),类似于输出电压KVO (155:1)。
一个12位逐次逼近型模数转换器(SAR ADC)差分检测线电压。 -3.3 V 至 3.3 V范围内的模拟信号将转换为0 至 4096范围内的整数。有效ADC增益为(4096 / 6.6)。
增益因子KM显示为代表任何前馈函数或归一化。 在此仿真中,不使用线性前馈。
对于电流检测,使用了10位SAR ADC,外部电流检测增益为0.62。 这为我们提供了数字电流基准(IREF)和电感器电流(IL)之间的关系: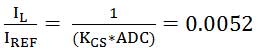
对于输出电压检测,使用了10位SAR ADC。
2.2 nF电容器置于反馈电阻分压器上,提供一个用于抗混叠的低通RC滤波器。 分压器中的上部电阻= 4160 kΩ。 分压器中的下部电阻= 27 kΩ。
关断频率是:
我们采样10 kHz处的反馈电压。
我们可用一个陷波滤波器使控制电压 (电压补偿器的输出) 或反馈电压信号上出现的2x线性频率纹波衰减。 由于采用控制电压生成内部电流回路控制的电流基准,因此这基准更精确,从而使系统性能(PF,THD)更佳。
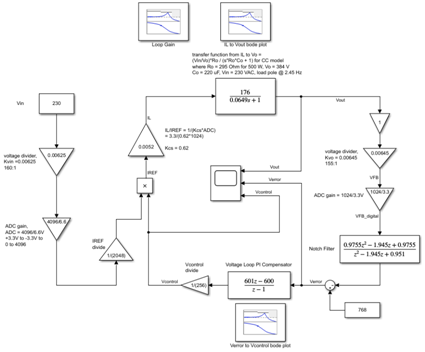
图4:恒定电流的受控模型电压回路Simulink框图
对于恒定电阻模型,补偿零点的最佳位置是在受控极点处[2]。 输出电容的大小通常取决于保持时间要求。 一般的经验法则是每瓦 0.5至1 µF。对于500 W设计,输出电容为440 µF是合理的。 为了消除负载极点,补偿零点在2.5 Hz处。 对于此仿真,选择的输出电容为220 µF,若是恒定电阻模型,其负载极点在4.9 Hz处,若是恒定电流负载,其负载极点在2.45 Hz处。
流程是绘制受控对象传递函数,设置补偿零点,并调整补偿器增益以达到目标交越频率。
S域PI补偿器的零点补偿在2.5 Hz处,且在0.1 Hz处的增益是40 dB: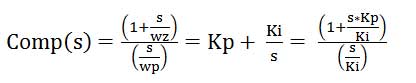
原点的极点由下式得出:
wp = Ki, wz = Ki/Kp
wz = 2*pi*2.5 = 15.7 rad/s
wp = 2*pi*10 = 62.8 rad/s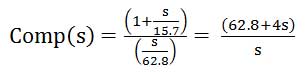
现在,使用后退欧拉法和100 µs的采样时间: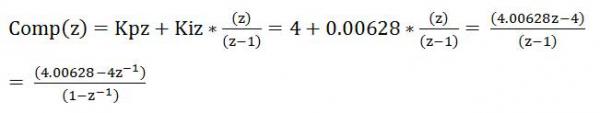
与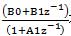 相比,,系数是:
相比,,系数是:
B0 = 4.00628, B1 = -4, A1 = -1
除以23使系数在-1到+1范围内。 然后乘以215:
B0 = 4.00628 * 4096 = 16,409.723 = 16410
B1 = -4 * 4096 = -16384
A1 = -1 * 4096 = -4096
所用的微分方程式变为:
U(n) = U(n-1) + 16410*E(n) – 16384*E(n-1) -> 记得除以212
或,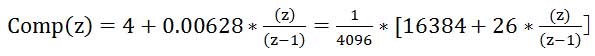
Kpz = 16384, Kiz = 26, 除数= 4096
表4:几个不同的电压补偿器,具有不同的零点位置和DC增益
|
后退欧拉法变换, |
零点位置 |
0.1 Hz处的增益 |
100 Hz处的增益 | |
|
(a) |
Kpz=16384, Kiz=26, 除数=4096 |
2.52 |
40 |
12.1 |
|
(b) |
Kpz=600, Kiz=1, 除数=256 |
2.65 |
35.8 |
7.41 |
|
(c) |
Kpz=800, Kiz=1, 除数=128 |
1.99 |
41.9 |
15.9 |
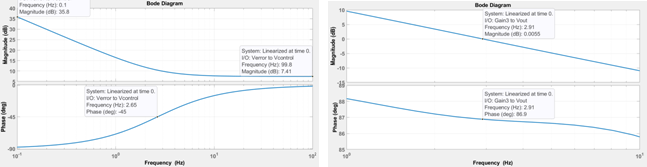
图5:(b)的电压回路PI补偿器波特图,整体波特(180 VAC, 恒定电流模型)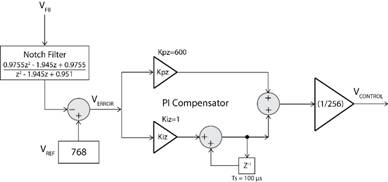
图6:(b)的电压回路补偿器
表5:不同负载模型和补偿器的电压回路带宽和相位裕度
|
电压补偿器 |
交越频率和相位裕度 (PM) | |||||
|
恒定电阻模型 |
恒定电流模型 |
恒定功率模型 | ||||
|
180 VAC |
230 VAC |
180 VAC |
230 VAC |
180 VAC |
230 VAC | |
|
Kpz=600, Kiz=1, 除数=256, |
1.7 Hz (103º PM) |
3.25 Hz (106º PM) |
2.9 Hz (87º PM) |
4.65 Hz (86.7º PM) |
3.52 Hz (52º PM) |
5.16 Hz (61º PM) |
|
Kpz=800, Kiz=1, 除数=128, |
1.98 Hz (112º PM) |
4.49 Hz (112º PM) |
3.51 Hz (94º PM) |
5.92 Hz (92º PM) |
4.15 Hz (63º PM) |
6.4 Hz (70.7º PM) |
|
Kpz=800, Kiz=1, 除数=128, |
6.12 Hz (109º PM) |
11.3 Hz (100º PM) |
7.34 Hz (91º PM) |
12.1 Hz (88º PM) |
7.73 Hz (73º PM) |
12.3 Hz (77º PM) |
电流回路分析
电感电流传递函数的小信号占空比由[7]得出: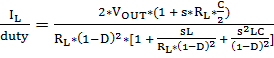
应用高频近似值[7] :![]()
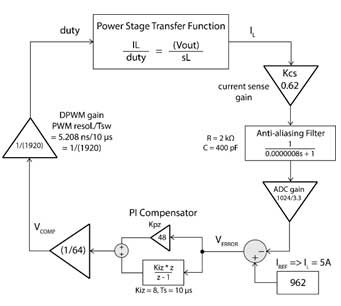
图7:电流回路框图
系统参数L = 500 µH, VO = 384 V,我们有:![]()
原点的极点在122 kHz、0 dB处交越
电流检测增益是0.62
低通RC滤波器用作抗混叠滤波器。
R = 2 kΩ, C = 400 pF
关断频率是:![]()
电流基准生成,IREF:
电流基准是电压控制回路(VCONTROL)的输出和瞬时线性电压检测(VLINE)的乘积。基准电流水平随负载需求增加而升高。
为了分析电流回路的动态特性,IREF保持恒定。 它在所关注回路之外,其大小不起作用。
数字脉宽调制(PWM)增益:
电流回路补偿器的输出存储在16位比较寄存器中。 模块的基本计时器/计数器越过比较值后,数字PWM输出就会切换。 基本定时器分辨率由外设时钟配置决定。 PWM时钟设置为192 MHz,对应于5.208 ns的占空比分辨率。 所需的PWM开关频率是100 kHz。因此,比较寄存器值1920对应于100%占空比。 实际上,有一个最大占空比,设置为约97%。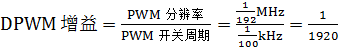
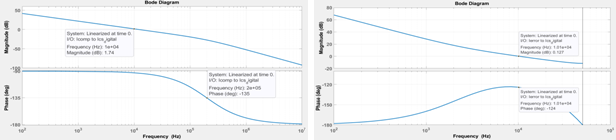
图8:未补偿的(左图)和补偿的(右图)电流回路波特图
电流回路的目标带宽通常约6至10 kHz。 上面的未补偿波特图从Icomp到Ics_digital的区域表明,在10 kHz的目标交越频率下,回路增益已接近0 dB。 电流补偿器无需在该区域提供任何增益。 我们可将补偿零点设置得足够低,以提供在10 kHz下所需的相位提升。
由于系统是一阶的,因此使用一个简单的PI补偿器就可以了,含在原点的一个极点和一个所需位置的零点。
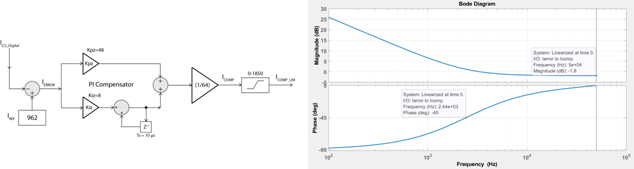
图9:电流回路PI补偿器和波特图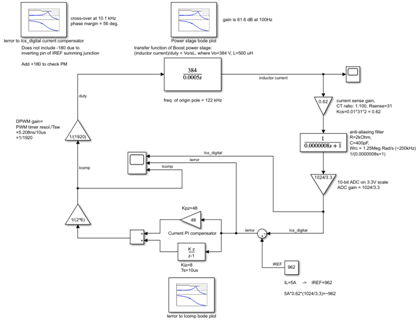
图10:电流回路Simulink框图
表6:几个电流回路补偿器,具有不同零点位置及由此产生的带宽和相位裕度
|
电流补偿器值,带1/64 后缩放 |
零点位置 |
交越频率和相位裕度 | |
|
示例(a) |
Kpz=48, Kiz=1 |
328 |
9.24 kHz, 69 deg. |
|
示例(b) |
Kpz=48, Kiz=4 |
1270 |
9.56 kHz, 63 deg. |
|
示例(c) |
Kpz=48, Kiz=8 |
2440 |
10.1 kHz, 56 deg. |
|
示例(d) |
Kpz=48, Kiz=12 |
3500 |
10.7 kHz, 50 deg. |
最终选择的电流回路PI补偿器是示例(c):Kpz=48, Kiz=8,带 1/64 后缩放
Simscape模型
我们设计好补偿器后,可将它们用于下图11所示的Simscape模型中,以观察稳态波形、电感器电流纹波、输出电压纹波,瞬态性能等。滤波后的线性电流传输到THD模块以粗略衡量失真。
图12显示了稳态时的仿真波形:电感电流、输出电压、电流回路补偿器的输出和THD。
实验验证
我们评估了图13所示的500 W图腾柱无桥PFC板的性能。图腾柱PFC与上述单通道电流控制模式(CCM)升压PFC的稳定性分析和补偿器设计无异。

图13:500 W图腾柱PFC评估板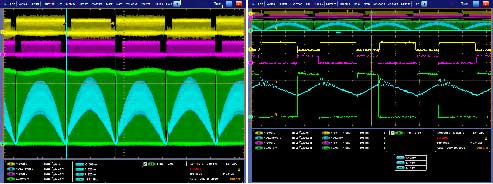
图14:180 VAC, 540 W, 60 Hz, PF=0.995, THD <3%
图14显示示波器捕获的电流检测信号 (蓝色)、开关节点(绿色)、快速支路PWM驱动输出 (黄色和紫色)。
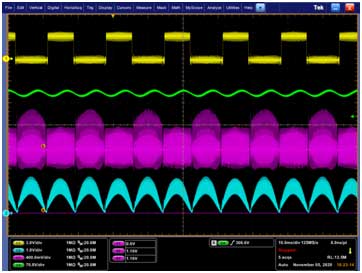
图15:180 VAC, 500 W
图15显示示波器捕获的电流检测信号(蓝色)、输出电压(绿色)、慢速支路低边驱动SRLO (黄色)及电压回路补偿器输出(Vcontrol DAC,紫色)。

图16:波特图:仿真与在180 VAC、500 W, 恒定电流模式的测量值的对比
图16将采用Simulink仿真的预期带宽和相位裕度与使用频谱分析仪的实际测量值进行了比较。 图表很吻合。
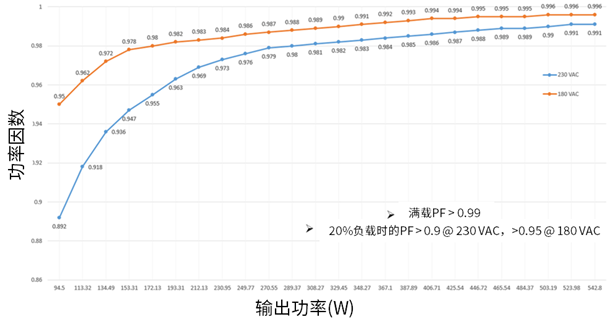
图17:功率因数对比输出功率
图17显示了在180 VAC和230 VAC两种不同线性电压水平、不同负载下的功率因数。
总结:
Simulink和Simscape已用于分析500 W服务器电源应用的平均电流模式控制的功率因数校正电路。 我们在一块原型板上验证了所选的仿真参数。
分享到:
猜你喜欢