
“随着汽车电子技术的发展,轻量化与智能化的需求也带动了英飞凌智能功率器件 (IPD)在车身负载驱动的大规模应用。对于感量较大的负载,如雨刮、鼓风机、风扇、继电器等,需要考虑负载关断时产生的能量对系统的冲击,同时驱动器件不能被该能量击穿。本文提供了评估测量感性能量的方法和工具,在一个明确定义的应用场景中,瞬间关断时的产生的箝位能量(ECL),与高压侧器件本身的能量能力进行对比,保证IPD器件长期可靠工作。
”本文由英飞凌任宝栋,与联合电子汽车洪 炜、薛洋、张久庆联合撰写,并发表于《汽车实用技术》2022年第十一期。
摘要
随着汽车电子技术的发展,轻量化与智能化的需求也带动了英飞凌智能功率器件 (IPD)在车身负载驱动的大规模应用。对于感量较大的负载,如雨刮、鼓风机、风扇、继电器等,需要考虑负载关断时产生的能量对系统的冲击,同时驱动器件不能被该能量击穿。本文提供了评估测量感性能量的方法和工具,在一个明确定义的应用场景中,瞬间关断时的产生的箝位能量(ECL),与高压侧器件本身的能量能力进行对比,保证IPD器件长期可靠工作。
1 简介
退磁过程介绍
汽车应用越来越需要具备驱动大电流、大感量执行器的能力,在变速箱控制模块(TCU)应用中,常用的执行器如电机、电磁阀(净化、进气)等;在车身控制模块(BCM)中,常用的执行器如雨刮、继电器或风机、水泵、油泵也同样表现为感性特点。驱动这些负载最简单和最常见的方法是将它们连接到高边侧开关的输出,如图1所示(器件集成的诊断和保护功能未在框图内显示)。
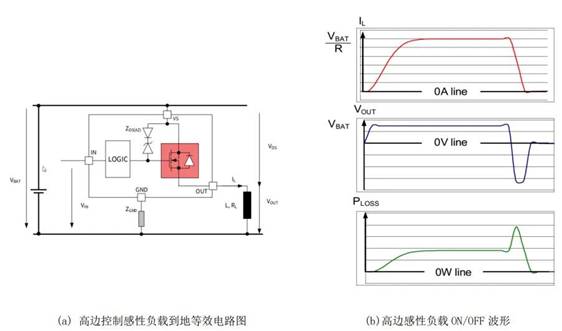
图 1 高边控制模块框图与等效电路
在开关的导通阶段给感性元件充电时,存储的能量与负载电流(IL)和电感(L)有关,如下所示:
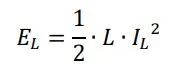
在开关断开之后,负载电流将降至零,之前存储的能量加上VBAT产生的能量将同时耗散:能量较小时,将通过热的形式消耗到负载本身(RL);当能量较大时,大部分能量将被IPD内置钳位二极管吸收,从而保护IPD芯片与负载。通常,工程上可以实施不同的技术以减少这种施加到IPD内部的耗散能量,如通过使用续流二极管或RC并联支路等。但是,以上方法除了增加成本与系统复杂程度之外,还会延长执行器的关闭时间(tF)。
在某些应用场合下,例如:喷油器驱动、PWM控制阀等,对关闭时间有严格的要求。因此,IPD所具备主动钳位的功能,使其成为一个非常完美的解决方案。通常,IPD所具备的箝位电压(VCL)越高,其关闭时间tF将越短。并且,能量在箝位期间耗散到IPD内置TVS中,称之为箝位能量(ECL),对于大功率应用场景中,通常都具备更多能量冲击,会在器件硅中产生重复的热应力,从而影响器件寿命以及其它功能等。
2 感性负载
2.1 工程应用时感性负载Ecl能量测量
评估实际负载特性并获得高边开关中耗散的箝位能量值的最佳方法是通过实际测量得到。当然,除了保证测量仪器的精准,尽可能多地再现执行器的操作条件是很重要的,这样更能贴近实际应用中情况。如图2所示,钳位能量的测试,建议将负载保持在试验箱内预期的工作温度下进行测量。
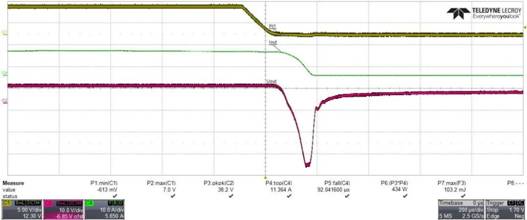
图 2
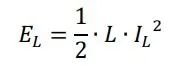
钳位能量表示为:
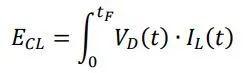
其中VD和IL分别是开关电压和负载电流,tF是负载电流关闭后归零需要的时间。

1)通过LCR测量确定的标称值
2)器件特性通过英飞凌官方数据手册获得
现在我们来看一个真实的例子:利用时下常见的数字示波器的数学函数,很容易得到被测VD、IL及其积分的乘积,如图3所示。
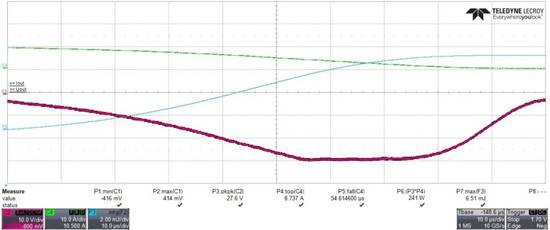
图3 ECL测量(RL=0.53Ω,LL=206uH,VBAT=12V,TA=25°C)2
备注2 绿色C4为电流关断波形,紫色C2为out引脚负压波形,蓝色F2为C2*C4在关断时间内的积分。
结果如下:
–VCL=38.2V
–IL=11.3A
–tF=92微秒
–ECL=6.51mJ
工程应用中,通常直接将电流等效成线性函数进行近似求解,公式计算如下:
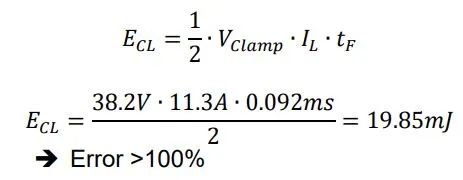
如果我们将近似值与实测值进行比较,很明显我们可以看到误差高于100%。
2.2 ECL理论模型分析和计算
将IPD内部集成主要元器件分离,考虑ON与OFF时两种状态,其等效电路如图4所示。
ON状态时,负载IL电流如公式(1):
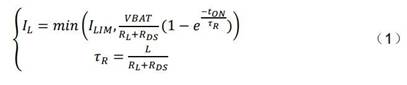
τR是电感电流上升的时间常数
ILIM是IPD器件本身的限制电流,tON是执行器的开启持续时间。等式(4)除了包括开关电流保护的可能干预之外,我们还考虑了这样一个事实,即短时间接通不会给负载足够的时间来达到其状态电流。
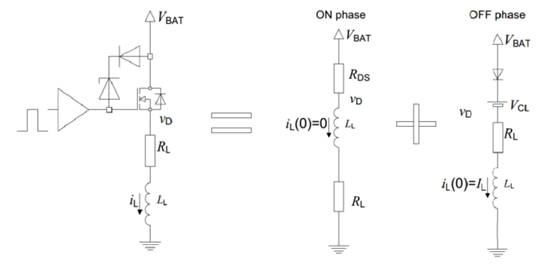
图 4 等效电路
2.2.1 齐次微分方程求解
输出关断时,电路的等效微分方程为
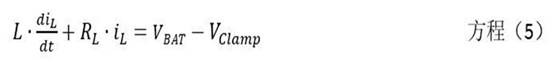
以iL(0)=IL为初始条件求解方程(5),得到电感电流的动态方程。
对一阶线性齐次微分方程求通解,电感电流按指数规律衰减,衰减的快慢取决于电感自身机电常数τ。VBAT-VClamp=0,待求解微分方程如下:
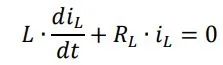
提取特征方程为
![]()
求得特征解为
![]()
然后再求得通解为
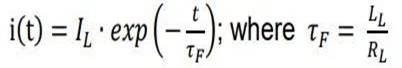
得到通解,也就是暂态分量,继续求特解,也即稳态解。
2.2.2 非齐次微分方程求解
动态电流方程为
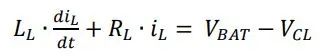
三要素法,恒定激励下一阶微分方程的解的一般形式为
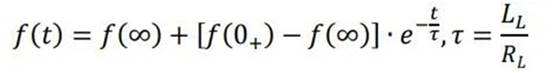
据此求得电流的动态方程表示为:
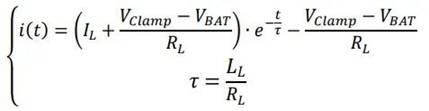
令
分享到:
猜你喜欢