
“在 RF 应用中,我们通常处理非常微弱的信号,这些信号很容易被我们电路中产生的噪声所掩盖。噪声电平终决定了接收器能够可靠检测到的信号。因此,RF 组件和系统的噪声特性至关重要。在我们关于噪声系数的介绍性文章中,我们了解了如何使用该指标来表征 RF 组件的噪声性能。
”在 RF 应用中,我们通常处理非常微弱的信号,这些信号很容易被我们电路中产生的噪声所掩盖。噪声电平终决定了接收器能够可靠检测到的信号。因此,RF 组件和系统的噪声特性至关重要。在我们关于噪声系数的介绍性文章中,我们了解了如何使用该指标来表征 RF 组件的噪声性能。
现在我们已经熟悉了基本概念,我们可以仔细研究一下噪声系数的定义,并讨论一些有时不够突出的细微之处。这应该可以帮助您避免对本规范的错误解释。
噪声系数定义和噪声因数方程
电路的噪声因数 (F) 可定义为:
F=NoGNiF=NoGNi
等式 1。
在哪里:
No 是输出端的总噪声,包括电路内部噪声源的影响和来自源阻抗的噪声
N i 是源阻抗在电路输入端产生的噪声
G是阶段的功率增益
虽然这个解释是正确的,而且实际上在一些参考资料中也提供了类似的解释,例如Paul R. Gray广泛使用的 教科书“模拟集成电路的分析与设计”第 4 版,但它并没有提供所有的细节噪声系数定义。根据IEEE 定义,N i 是源电阻器在 T 0 = 290 K°(或 16.85 °C)温度下的可用热噪声功率。这个温度比舒适的室温要低一点;但是,有时在 RF 工作中将其称为室温。
此外,IEEE 定义指出,No是 设备输出端的可用噪声功率,G 是设备的可用功率增益。这里的关键点是规范的参考温度 T 0 = 290 K°,以及用于描述方程式 N i、 N o和 G 的所有三个参数的描述符“可用”。在本文的其余部分,我们将详细讨论“T 0 = 290 K 时的可用噪声功率”的含义。
可用噪声功率
热激发电荷载流子的随机运动表现为电阻器中的噪声。噪声电阻器可以通过添加与无噪声电阻器串联的噪声电压源来建模,如下图 1 所示。
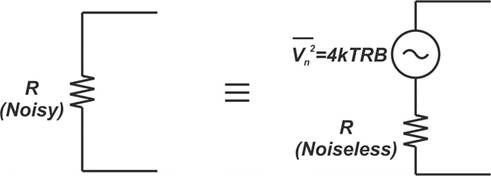
图 1. 噪声电阻示例图以及添加与无噪声电阻串联的噪声电压源。
噪声电压源的PSD(功率谱密度)为 ( overline {V_n^2} = 4 space kTRB),其中:ˉ ˉˉˉˉˉ ˉ V 2 n =4kTRB Vn2ˉ=4 kTRB
k 是玻尔兹曼常数 (1.38 × 10 -23 Joules/Kelvin)
T 是开尔文温度
B 是考虑的带宽(赫兹)
在噪声系数定义中,N i 是源电阻的可用噪声功率。现在的问题是,图 1(b) 中的电路可以提供的噪声功率是多少?根据基本电路理论,我们知道当负载电阻等于源电阻时传输的功率。因此,可以使用以下电路(图 2)找出源电阻 R S的可用噪声功率。
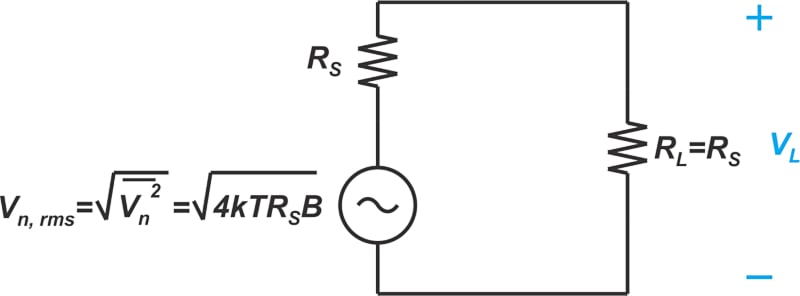
图 2. 用于查找源电阻器可用噪声功率的电路图。
请记住,我们 在上图中使用了噪声源的RMS(均方根)值。由于一半的噪声电压出现在负载两端,因此传输到匹配负载的噪声功率 R L = R S可以通过以下公式找到:
P L = V 2 L R L=( V n ,均方根米秒2) 2×1大号_=4 k T R S B 4× 1秒_=k T BPL=VL2RL=(Vn,rms2)2×1RL=4kTRSB4×1RS=kTB
等式 2。
这是噪声系数计算的重要结果。请注意,可用噪声功率与电阻值无关。无论是 1 mΩ 电阻还是 1 MΩ 电阻,可用的噪声功率都是 kTB。在 1 Hz 带宽中,可用噪声功率为 kT。噪声系数定义基于 T 0 = 290 K 时的可用噪声功率 。以 dB表示 kT 0时,此参考温度下的可用噪声功率为 -174 dBm/Hz,计算如下:
10 l o g ( k T 0 ) = 10 l o g ( 1.38 × 10 ? 23 × 290 ) ≈ ? 174 d B m 10log(kT0)=10log(1.38×10?23×290)≈?174 dBm
噪声系数指定添加噪声的相对量
由于噪声系数定义基于 N i = kT 0 B,因此它指定了相对于 N i添加到信号中的噪声的相对量。考虑我们在上一篇文章中推导出的以下噪声系数方程:
F = 1 + N o ( a d d e d ) N o () _ _ _ _ _F=1+No(added)No(source)
这里,No (source) 是源于源阻抗的输出噪声的一部分;No (added) 是电路本身产生的输出噪声的一部分——不包括源电阻贡献。注意 N o(source) = kT 0 BG,我们得到等式 3:
F = 1 + N o ( a d d e d ) k T 0 B GF=1+No(added)kT0BG
等式 3。
为了更好地形象化上述等式的噪声项,请考虑图 3 中的下图,有时称为“噪声线”。

图 3. 显示噪声线的图。
在上图中,总输出噪声 No 相对于源电阻温度 T 绘制。如果 R S 无噪声(或 T = 0 K),输出端出现的噪声将是被测设备或 No o(added)。当我们提高 R S的温度时,它的噪声贡献会增加。对应于 T = T 0的噪声系数度量实际上指定了 R S 在 T 0时贡献的输出噪声(即 kT 0 BG)与被测设备的输出噪声 (No (added) ) 之比。例如,如果系统的噪声系数为 F = 2(或 NF = 3 dB),我们知道 No (added) 等于 kT 0 BG。
如图所示,R S 噪声与 No (added)的比值 不是恒定的,而是随 T 变化的。因此,如果 R S 处于 T 0以外的温度,我们不能直接使用噪声系数方程来计算找到输出噪声。 相反,我们应该首先找到来自 DUT(被测设备)的噪声,加上感兴趣温度下 R S的噪声,计算总输出噪声。
我们还可以通过将分数的分子和分母除以级的功率增益,根据输入参考噪声值来表达等式 3。这产生了等式 4:
F = 1 + N i (加d e d ) N i _F=1+Ni(added)Ni
等式 4。
在这个等式中,N i(added) 是由 DUT 贡献的输入参考噪声,N i 是源在 290 K 时的可用噪声功率。同样,如果 F = 2,则输入参考噪声由DUT 等于 N i = kT 0 B。让我们看一个例子来阐明这些概念。
示例:使用噪声系数方程
放大器的噪声系数、带宽和增益分别为:
噪声系数 = 2.55 分贝
B = 10 兆赫
增益 = 5.97 分贝
假设可用输入噪声为 kT A B,找出两种不同情况下的输出噪声:1 - T A = 290 K 和 2 - T A = 150 K。
我们首先找到噪声系数和增益的线性值:
F = 10 N F 10= 10 0.255 = 1.8F=10NF10=100.255=1.8
G = 10 G a n 10 _= 10 0.597 = 3.95G=10Gain10=100.597=3.95
由于噪声系数的定义假设输入噪声是 T = 290 K 时的可用噪声功率,我们可以直接从等式 1 求出该温度下的输出噪声:
N o = N i FG=k T 0 B×FGNo=NiFG=kT0B×FG
以分贝表示右侧,我们有:
否_=10 l o g ( k T 0 ) + 10 l o g ( B F G )=? 174 d B m / H z + 10 l o g ( 10 × 10 6 × 1.8 × 3.95 ) =? 95.48分贝米_ No=10log(kT0)+10log(BFG)=?174 dBm/Hz+10log(10×106×1.8×3.95)=?95.48 dBm
对于 T A = 150 K,我们不能直接使用噪声系数方程。然而,噪声系数方程可用于计算系统产生的噪声。将 N i = kT 0 B 代入等式 4,系统产生的输入参考噪声为:
N i ( a d d e d ) =(F?1)k T 0 BNi(added)=(F?1)kT0B
当 F = 1.8 时,我们得到 N i(added) = 0.8kT 0 B。因此,输入端的总噪声为:
N i ( t o t a l ) = N i ( a d d e d ) +k T A B= 0.8 k T 0 B + k T A BNi(total)=Ni(added)+kTAB=0.8kT0B+kTAB
将该值乘以系统增益 G,即可得到总输出噪声功率。在下面的等式中,我将 T A写成 T 0 以简化计算:
没有(总计)_ _ _ _ _=G ( 0.8 k T 0 B + k T A T 0 T 0乙)=G k T 0 B ( 0.8 + 150 290)No(total)=G(0.8kT0B+kTAT0T0B)=GkT0B(0.8+150290)
以分贝表示右侧,我们有:
没有(总计)_ _ _ _ _=10 l o g ( k T 0 ) + 10 l o g ( B G × 1.317 )=? 174 d B m / H z + 10 l o g ( 10 × 10 6 × 3.95 × 1.317 ) =? 96.84分贝米_ No(total)=10log(kT0)+10log(BG×1.317)=?174 dBm/Hz+10log(10×106×3.95×1.317)=?96.84 dBm
如果不注意噪声系数的定义,可能会将 N i = k × 150 × B 代入等式 1,这会产生不正确的结果 No = -98.34 dBm。
物理温度或噪声温度
在上面的讨论中,我们强调了源电阻 R S的物理温度对我们的 NF 计算的影响。通常情况下,驱动点阻抗 (R S ) 与 DUT 处于相同的物理温度;然而,电路接收到的输入噪声功率高于 kT 0 B。这通常发生在级联系统中,信号链中的每个模块都会增加本底噪声。因此,级联中下游级的输入噪声通常超过 kT 0 B。在这些情况下,我们也无法通过直接应用噪声系数方程来计算输出噪声电平。相反,我们可以先使用 NF 方程来计算电路产生的噪声 (N i(added)),然后使用该信息和输入噪声电平来计算总输出噪声。 此外,定义输入噪声的等效噪声温度 T e也很有帮助。这是可用热噪声功率 (kT e B) 等于输入噪声功率时的温度。若输入噪声功率为N 1,其等效噪声温度为:
T e = N 1 k BTe=N1kB
噪声系数和等效噪声温度是组件噪声特性的可互换表征。在下一篇文章中,我们将查看使用噪声温度概念的示例。
噪声系数指定 SNR 劣化
噪声系数是电路引起的SNR(信噪比)退化的直接量度。这个说法是正确的;然而,它值得更多的解释。让我们再考虑上面讨论的例子。我们假设系统的噪声系数和增益分别为 NF = 2.55 dB 和增益 = 5.97 dB,并假设输入信号功率为 -40 dBm。当 R S 为 T A = 290 K 时,输入噪声功率为:
镍_=10 l o g ( k T 0 ) + 10 l o g ( B )=? 174 d B m / H z + 10 l o g ( 10 × 10 6 ) =? 104分贝米_ Ni=10log(kT0)+10log(B)=?174 dBm/Hz+10log(10×106)=?104 dBm
从示例的结果中,我们知道输出噪声功率为 -95.48 dBm。图 4 总结了该示例输入和输出端的信号和噪声功率。

图 4. 前面示例的输入和输出端的信号和噪声功率汇总。
输出信号功率由输入信号乘以放大器的功率增益得到。图 4 还提供了输入和输出 SNR,以及 SNR 退化。请注意,SNR i / SNR o的比值 等于噪声系数 NF = 2.55 dB,这并不奇怪,因为我们知道这个比值实际上是噪声系数的定义。但是,对于 T A = 150 K的情况呢?在这种情况下,输入噪声为 N i = -106.86 dBm。图 5 总结了前面示例的结果。
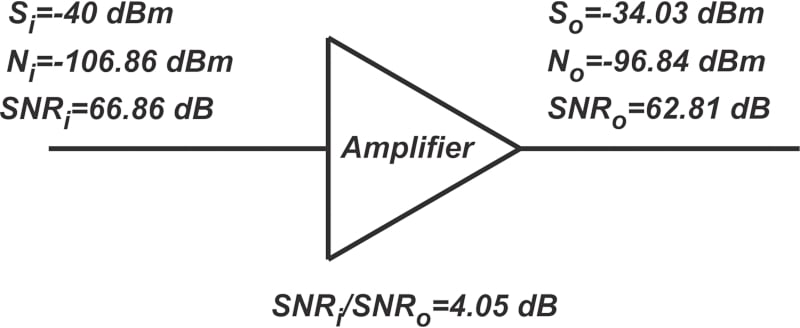
图 5. 上述示例的另一个结果汇总。
如您所见,SNR 退化 (SNR i / SNR o ) 现在大于 NF。这是因为输入噪声低于标准值,使得放大器的噪声贡献更加显着。因此,当输入噪声为 kT 0 B时,噪声系数决定了 SNR 的退化。例如,如果一个电路的噪声系数为 7 dB,并且该模块的输入噪声功率为 kT o B,则输出端的 SNR该块的 7 dB 小于输入 SNR。
在下一篇文章中,我们将继续讨论并了解 NF 定义中出现的“可用增益功率”。
分享到:
猜你喜欢